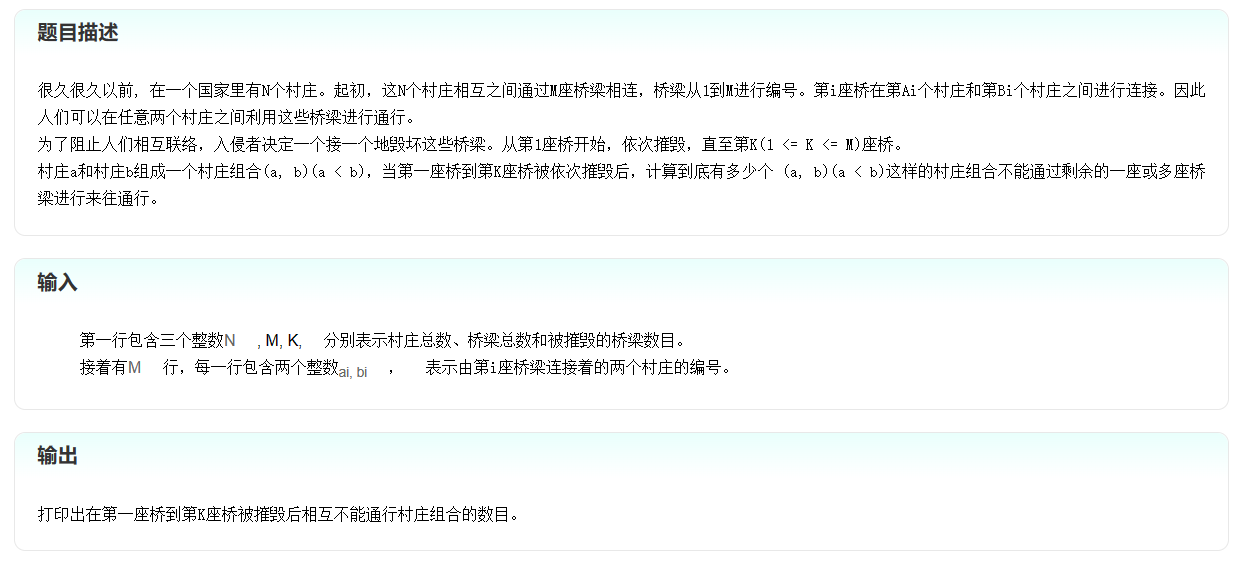
image _4_.png

1
2
3
4
5
6
4 5 3
1 2
2 3
3 4
4 1
1 3
1
3

数据范围：
2 <= N <= 10^5
1 <= K <= M <= 10^5
1 <= ai < bi <= N
所有的村庄组合(ai, bi) 各不相同。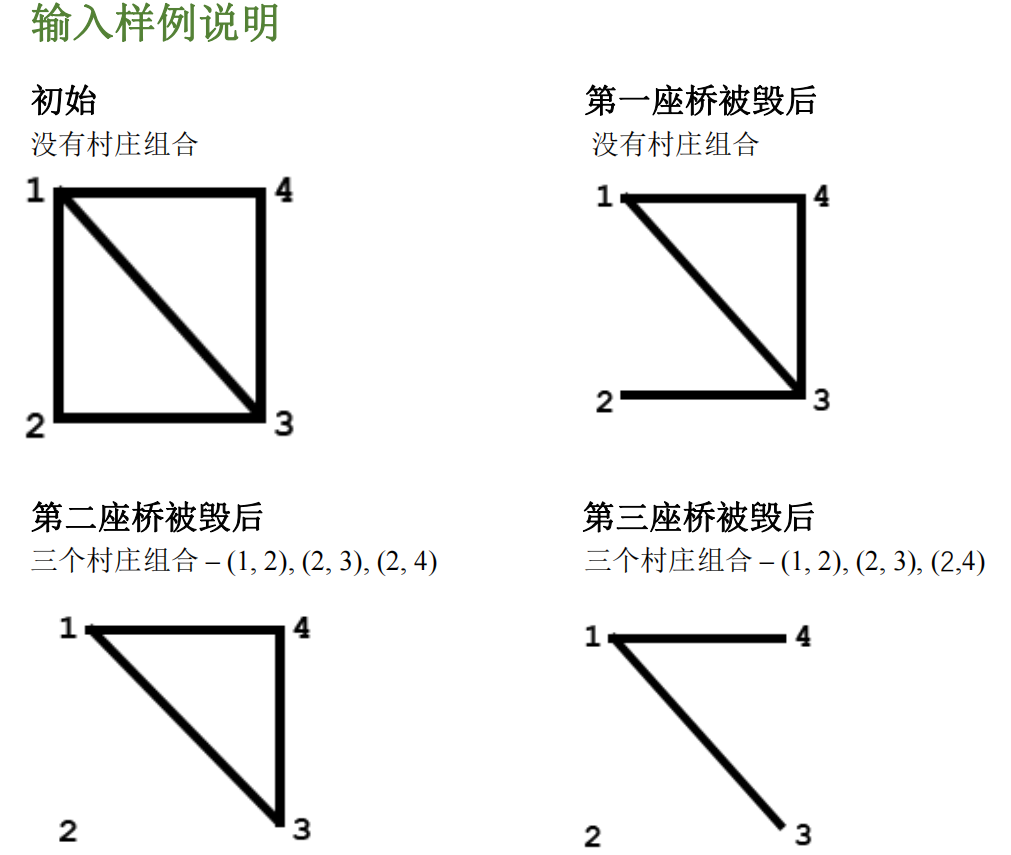
image.png
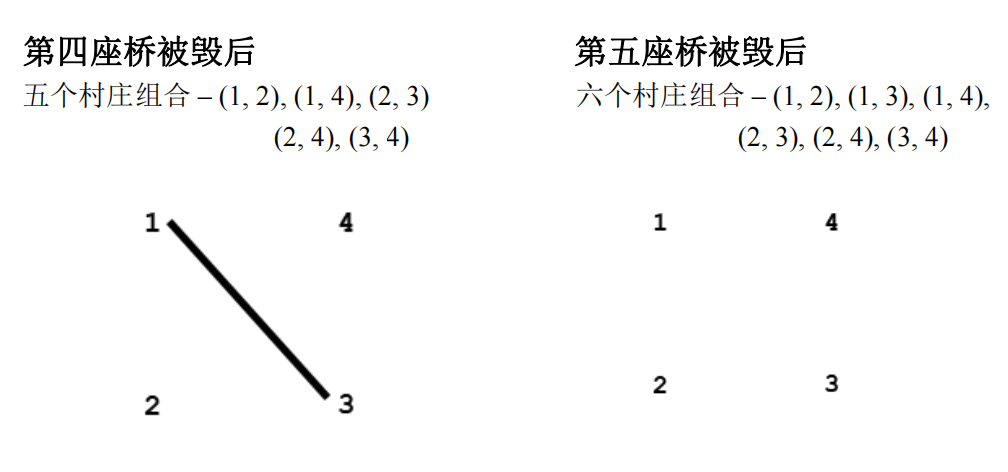
image _5_.png
将村庄看成点，桥看成边，显然一开始给你的一定是所有的点都可以通过某条边直接或者间接相连，那么村庄的组合就是$C_{n}^{2} = \frac{n*(n-1)}{2} $，即选出两个村庄进行组合。去除一些边后问你毁了多少个组合。所以思路就是求连通块，计算每个连通块有多少个点，用组合数的公式进行计算还剩下多少个点，计算之后再减去总的村庄组合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<bits/stdc++.h>
#define ll long long
#define M 100005
using namespace std;

struct Node {
    ll a, b;
} e[M];

ll n, m, k, par[M], cnt, a[M];
vector<ll> v;

ll find(ll x) {
    if (par[x] != x)par[x] = find(par[x]);
    return par[x];
}

void process() {
    for (ll i = 1; i <= cnt; ++i) {
        ll a = e[i].a, b = e[i].b;
        a = find(a), b = find(b);
        if (a != b) par[a] = b;
    }
    for (ll i = 1; i <= n; ++i) {
        ll t = find(i);
        if (t != i)a[t]++;
        //如果父亲不是自己，那么和别人肯定有一条边联通，累加这个父节点连接的结点数
    }
    for (ll i = 1; i <= n; ++i) {
        if (a[i] != 0)v.push_back(a[i] + 1);
        //如果该节点连了其他结点，那么就加上他自己压入vector里面
    }
    ll res = 0;
    for(auto &t:v){//遍历所有的连通块
        res += t*(t-1)/2;
    }
    ll all = n*(n-1)/2;
    cout<<all-res;//总的数量减去连通块的数量就是减少的村庄组合
}

int main() {
    cin.tie(nullptr), ios::sync_with_stdio(false);
    cin >> n >> m >> k;
    for (ll i = 1; i <= m; ++i) {
        ll ai, bi;
        cin >> ai >> bi;
        if (i <= k)continue;
        cnt++;
        e[cnt].a = ai;
        e[cnt].b = bi;
    }
    for (ll i = 1; i <= n; ++i)par[i] = i;
    process();
    return 0;
}