省赛补题,顺序大致按难度(赛时通过人数)排列
CF的gym里暂时还没有今年省赛的题目上传,目前只查到了D/F/G/H/I的补题链接
A.Look and Say
翻译:
给一个数字序列,你需要使用以下方法“描述”它:
1.每段划分成最大的连续相同的数字;
2 . 对于每段,将其替换为段的长度加段中的数字。例如,“0” 应替换为 “10”, ”9999999999“ 应替换为“109”
3.将替换的段连接在一起并输出
输入:
第一行包含一个整数n,范围是[1,1000],表示输入序列的长度;
第二行为一个长度为n的序列,表示原始序列
输出:
输出转换后的序列
签到题,就是相同连续的数字压缩成长度+数字的组合输出
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;int n, cnt = 1 ;char pre = '#' , t;signed main () freopen ("input.txt" , "r" , stdin); freopen ("my.txt" , "w" , stdout); cin.tie (nullptr ), cout.tie (nullptr ); ios::sync_with_stdio (false ); cin >> n; for (int i = 1 ; i <= n; ++i) { cin >> t; if (t == pre)++cnt; else if (pre != '#' ) { cout << cnt << pre; cnt = 1 ; } pre = t; } cout << cnt << t; return 0 ; }
E.Interval Sum
翻译
构造一个长度为n的排列,使其所有子序列的和中能够被n整除的子序列的个数最多,输出任意一种构造。
输入:
一个n,表示排列的长度
输出:
一行排列,空格分开排列中的元素
一道贪心题,猜想比较好想:考虑哪些数相加为n,有n,{1,n-1},{2,n-2}…..注意n是偶数时,要把n放排列的最前面或者最后面,并且最后没有{n/2,n-n/2}这种组合
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <bits/stdc++.h> using namespace std;int n, t;signed main () freopen ("input.txt" , "r" , stdin); freopen ("my.txt" , "w" , stdout); cin.tie (nullptr ), cout.tie (nullptr ); ios::sync_with_stdio (false ); cin >> n; t = n / 2 + (n & 1 ); if (!(n & 1 ))cout << n / 2 << ' ' ; cout << n << ' ' ; for (int i = 1 ; i < t; ++i) cout << i << ' ' << n - i<<' ' ; return 0 ; }
这道题P9573 「TAOI-2」核心共振 和它比较像,但更难一点
M.A Wine and Four Dishes
翻译:
Rice老师为自己准备了一场盛宴。宴会上有x瓶酒和y盘菜,这意味着他需要x杯和y盘。
有n个箱子。第i个盒子里有a杯子和b盘子。请帮助Rice老师确定他必须打开的最小数量的盒子,这样他才能收集到足够的杯子和盘子。如果Rice老师不可能收集到足够的杯子或盘子,那么输出“IMPOSSIBLE”。
输入
第一行包含了三个整数n,x,y表示箱子数,瓶子和盘子数
接下来n行表示每个箱子含有的瓶子和盘子数量
输出
最小数量的盒子,无解输出IMPOSSIBLE
贪心题,注意到每个箱子包含的盘子数是[0,1],所以如果x不是0,那么优先从含有x的箱子中选最大的那几个,选完了就选剩下的箱子中y最大的那几个,如果选完了都凑不出那么就是无解,数据很小,随便做都可以过
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 #include <bits/stdc++.h> using namespace std;struct Bottle { int a, b; } box[40 ]; int n, x, y, bound = 1 , t;signed main () freopen ("input.txt" , "r" , stdin); freopen ("my.txt" , "w" , stdout); cin.tie (nullptr ), cout.tie (nullptr ); ios::sync_with_stdio (false ); cin >> n >> x >> y; if (!(x || y)) { cout << 0 ; return 0 ; } for (int i = 1 ; i <= n; ++i) cin >> box[i].a >> box[i].b; if (x) { sort (box + 1 , box + 1 + n, [&](Bottle A, Bottle B) { return A.a > B.a || A.a == B.a && A.b > B.b; }); if (!box[x].a) { cout << "IMPOSSIBLE" ; return 0 ; } for (int i = 1 ; i <= x; ++i, ++bound) t += box[i].b; if (t >= y) { cout << x; return 0 ; } sort (box + bound, box + 1 + n, [&](Bottle A, Bottle B) { return A.b > B.b; }); for (int i = bound; i <= n; ++i) { t += box[i].b; if (t >= y) { cout << i; return 0 ; } } cout << "IMPOSSIBLE" ; } else { sort (box + 1 , box + 1 + n, [&](Bottle A, Bottle B) { return A.b > B.b; }); for (int i = 1 ; i <= n; ++i) { t += box[i].b; if (t >= y) { cout << i; return 0 ; } } cout << "IMPOSSIBLE" ; } return 0 ; }
比赛的时候还不知道sort还有这种写法,嫌写比较函数太复杂用优先队列和pair瞎搞做对的,有些队伍用搜索剪枝过的,好像背包也可以
F.Turn the Light oj 的评测
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;int n, pre, t;signed main () cin.tie (nullptr ), cout.tie (nullptr ); ios::sync_with_stdio (false ); cin >> n; int l = 1 , r = n; while (l <= r) { int mid = (l + 1 + r) >> 1 ; cout << "? " << l << endl; cin >> t; if (t == pre) { cout << "! " << l << endl; return 0 ; } pre = t; cout << "? " << mid << endl; cin >> t; if (t == pre) { cout << "! " << mid << endl; return 0 ; } if (pre > t) r = mid - 1 , l++; else l = mid + 1 ; pre = t; } return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 #include <bits/stdc++.h> #define random(a, b) ((a)+rand()%((b)-(a)+1)) using namespace std;int n, pre, t;bool st[1000006 ];int lLight, rLight, cnt;void get_num (char c, int x, int fav) ++cnt; if (c == '!' ) { if (x == fav && cnt <= 40 )cout << "Accept" << endl; else if (cnt > 40 )cout << "Time Limit Error" << endl, getchar (); else cout << "Wrong Answer" << endl, getchar (); } else { if (x > fav && !st[x]) { ++rLight; st[x] = true ; } if (x < fav && !st[x]) { ++lLight; st[x] = true ; } cout << abs (lLight - rLight) << endl; t = abs (lLight - rLight); } } void init () memset (st, false , sizeof st); n = pre = t = lLight = rLight = cnt = 0 ; } void solve () init (); n = random (1 , 1000000 ); int num = random (1 , n); cin.tie (nullptr ), cout.tie (nullptr ); ios::sync_with_stdio (false ); cout << n << endl; int l = 1 , r = n; while (l <= r) { int mid = (l + 1 + r) >> 1 ; cout << "? " << l << endl; get_num ('?' , l, num); if (t == pre) { cout << "! " << l << endl; get_num ('!' , l, num); return ; } pre = t; cout << "? " << mid << endl; get_num ('?' , mid, num); if (t == pre) { cout << "! " << mid << endl; get_num ('!' , mid, num); return ; } if (pre > t) r = mid - 1 , l++; else l = mid + 1 ; pre = t; } } signed main () for (int i = 1 ; i <= 1024 ; ++i) { cout << "正在运行第" << i << "个数据" << endl; solve (); } return 0 ; }
跑了很多组对拍发现其实这个算法能够在29次询问以内通过
K. Lazy but Diligent
这题的程序对拍目前只验证了树这一特殊图的情况dp[i - 1][course[k].p] && dist[course[k].p][course[j].p] + course[k].b <= course[j].arestT = max(course[j].a - course[k].b - dist[course[k].p][1] - dist[1][course[j].p], 0)course[j].b + dist[course[j].p][1] <= t && (t - course[j].b - dist[course[j].p][1]) + restT + rest[i - 1][k] >= sdp[i][course[j].p] = max(dp[i][course[j].p], dp[i - 1][course[k].p] + 1)rest[i][j] = min(s, max(rest[i][j], rest[i - 1][k] + restT))ans = max(ans, dp[i][course[j].p])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 5 4 3 10 2 3 4 1 2 5 1 4 5 1 3 1 1 2 9 2 3 9 4 6 8 3 output:1 5 4 4 15 3 3 4 1 4 1 1 5 2 2 5 3 2 5 6 4 8 9 3 13 14 2 4 6 5 output:2 hack: 6 5 1 5883 1327 2 1 43 3 2 8 4 3 48 5 2 37 6 2 43 1398 5257 2 output:1 7 6 5 3760 1835 2 1 2 3 2 16 4 2 53 5 2 89 6 2 61 7 6 49 320 1728 4 437 2046 2 1950 2242 6 3754 3758 3 1689 3242 5 output: 1 6 5 3 1967 1249 2 1 40 3 1 72 4 3 93 5 1 49 6 3 36 1651 1928 5 591 770 6 1557 1612 4 output:1 大样例: 155 154 126 3118 1830 2 1 7 3 2 10 4 2 7 5 1 66 6 2 89 7 6 42 8 4 81 9 3 59 10 1 28 11 8 33 12 4 38 13 3 70 14 3 93 15 13 71 16 15 28 17 2 87 18 8 41 19 4 67 20 13 12 21 15 27 22 15 59 23 15 72 24 4 6 25 11 59 26 12 12 27 8 57 28 15 50 29 15 51 30 4 18 31 1 82 32 3 66 33 3 35 34 10 28 35 5 89 36 14 70 37 5 22 38 15 93 39 10 52 40 29 8 41 25 10 42 26 103 43 39 36 44 7 65 45 21 71 46 37 91 47 11 67 48 8 52 49 32 91 50 31 46 51 10 83 52 19 58 53 42 77 54 31 85 55 30 31 56 2 37 57 31 104 58 26 20 59 55 14 60 47 73 61 60 27 62 12 43 63 36 36 64 19 95 65 33 71 66 27 3 67 17 99 68 29 4 69 17 32 70 63 64 71 44 51 72 20 25 73 31 47 74 65 23 75 43 29 76 50 5 77 59 63 78 60 17 79 30 86 80 41 32 81 3 15 82 26 72 83 80 2 84 39 49 85 66 40 86 22 26 87 5 7 88 38 91 89 22 96 90 36 4 91 52 52 92 66 99 93 52 54 94 1 73 95 67 1 96 6 21 97 65 23 98 90 91 99 42 32 100 75 55 101 90 47 102 10 1 103 32 77 104 47 86 105 5 76 106 83 50 107 90 3 108 52 88 109 10 72 110 40 96 111 71 71 112 45 10 113 21 85 114 21 56 115 15 80 116 40 59 117 34 78 118 60 66 119 114 47 120 64 24 121 72 19 122 101 68 123 46 27 124 55 17 125 22 13 126 8 12 127 49 96 128 70 28 129 58 35 130 108 21 131 58 65 132 40 9 133 100 37 134 65 73 135 74 76 136 17 54 137 42 63 138 21 32 139 44 102 140 45 91 141 17 40 142 120 56 143 74 78 144 31 1 145 12 75 146 47 46 147 26 86 148 30 14 149 115 69 150 32 12 151 57 87 152 106 20 153 110 57 154 139 3 155 121 60 1889 2840 127 2328 2789 9 1254 1456 52 2231 3048 25 1937 2019 96 71 117 91 556 1318 79 2029 2616 33 363 1158 29 60 1979 40 2938 2971 95 1506 2530 15 484 1232 13 2142 2273 94 2418 3085 26 1456 2049 69 409 2793 81 2506 2876 122 1694 2651 43 2734 3020 87 665 1578 134 1107 1681 145 2654 3059 73 387 1226 143 1957 2556 133 1355 1893 93 995 1661 152 1011 2205 51 1251 2780 58 2251 2374 121 1824 1847 54 504 1866 42 738 2361 154 1233 1627 78 1330 2763 68 1994 2048 18 1636 2392 66 17 2079 155 1324 2415 45 675 1181 129 1536 2185 108 1332 1752 57 1307 2932 85 1078 1130 99 902 982 24 1791 2453 21 1528 2256 148 3032 3047 114 1493 3016 103 1298 2529 104 434 2578 63 1682 2611 36 1722 3056 5 350 2091 20 1822 2810 62 1196 1885 38 486 1738 105 722 1375 17 495 1559 120 262 837 37 404 2209 124 1621 2570 89 1966 2783 65 2970 3024 50 2020 3033 136 1410 1559 83 504 1481 90 288 1350 97 755 1289 117 1232 1552 80 2967 3025 70 1695 2304 106 2874 2900 109 1257 3109 56 1900 2510 101 2535 2961 32 2636 2975 48 2951 2962 14 2964 2994 130 1325 1407 35 60 523 88 1701 2273 12 710 2279 31 557 668 76 2459 2546 111 2925 3092 119 700 2041 128 2117 2311 125 2152 2252 126 1646 2038 8 1867 3039 102 2341 2360 34 906 1225 86 1270 1906 150 267 2672 39 1684 1807 55 1622 1746 149 170 1839 142 1234 2035 132 3045 3065 151 1832 2659 2 2800 3045 110 56 1396 135 2119 3050 140 218 299 118 1911 2022 41 1737 2205 137 2694 2728 27 1661 2797 72 1662 2828 131 49 390 146 2206 2350 3 293 331 10 1784 2204 47 43 192 74 596 769 46 2109 2766 144 2992 3050 22 2381 3024 123 2156 2873 107 67 1236 67 717 726 98 2357 2483 4 211 686 100 1506 2983 116 1196 1301 77 output:6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 #include <bits/stdc++.h> #define N 405 using namespace std;int dist[N][N], dp[N][N], n, m, q, t, s, ans;int rest[N][N];struct Node { int a, b, p; } course[N]; void floyd () for (int k = 1 ; k <= n; ++k) for (int i = 1 ; i <= n; ++i) for (int j = 1 ; j <= n; ++j) dist[i][j] = min (dist[i][j], dist[i][k] + dist[k][j]); } signed main () cin.tie (nullptr ), cout.tie (nullptr ); ios::sync_with_stdio (false ); cin >> n >> m >> q >> t >> s; memset (dist, 0x3f , sizeof dist); for (int i = 1 ; i <= m; ++i) { int a, b, c; cin >> a >> b >> c; dist[a][b] = dist[b][a] = min (dist[a][b], c); } floyd (); for (int i = 1 ; i <= q; ++i) { int a, b, c; cin >> a >> b >> c; course[i].a = a, course[i].b = b, course[i].p = c; } for (int i = 1 ; i <= q; ++i) { if (dist[1 ][course[i].p] <= course[i].a) { rest[1 ][i] = min (course[i].a - dist[1 ][course[i].p], s); if (t - (dist[course[i].p][1 ] + course[i].b) + rest[1 ][i] >= s) { ++dp[1 ][course[i].p]; ans = max (ans, dp[1 ][course[i].p]); } } } for (int i = 2 ; i <= q; ++i) for (int j = 1 ; j <= q; ++j) for (int k = 1 ; k <= q; ++k) if (dp[i - 1 ][course[k].p] && dist[course[k].p][course[j].p] + course[k].b <= course[j].a) { int restT = max (course[j].a - course[k].b - dist[course[k].p][1 ] - dist[1 ][course[j].p], 0 ); if (course[j].b + dist[course[j].p][1 ] <= t && (t - course[j].b - dist[course[j].p][1 ]) + restT + rest[i - 1 ][k] >= s) { dp[i][course[j].p] = max (dp[i][course[j].p], dp[i - 1 ][course[k].p] + 1 ); rest[i][j] = min (s, max (rest[i][j], rest[i - 1 ][k] + restT)); ans = max (ans, dp[i][course[j].p]); } } cout << ans; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #include <bits/stdc++.h> using namespace std;#define random(a, b) ((a)+rand()%((b)-(a)+1)) int dsu[1000005 ];int mapp[10000005 ];bool st[1000005 ];void build (int n) ofstream fout ("input.txt" ,ios::trunc) ; int q = random (1 ,n-1 ),t = random (3 ,10004 ); int s = random (0 ,t); for (int i = n; i >= 2 ; --i) { dsu[i] = random (1 , i - 1 ); } for (int i = 1 ; i <= n; ++i) mapp[i] = i; cout << n << ' ' << n-1 << ' ' <<q<< ' ' <<t<< ' ' <<s<< ' ' <<endl; fout << n << ' ' << n-1 << ' ' <<q<< ' ' <<t<< ' ' <<s<< ' ' <<endl; for (int i = 2 ; i <= n; ++i) { int temp = random (1 ,104 ); cout << mapp[i] << ' ' << mapp[dsu[i]] << ' ' <<temp <<endl; fout << mapp[i] << ' ' << mapp[dsu[i]] << ' ' <<temp<< endl; } for (int i = 1 ;i<=q;++i){ int p = random (2 ,n); while (st[p])p = random (2 ,n); int a = random (1 ,t-2 ); int b = random (a+1 ,t-1 ); cout<<a<<' ' <<b<<' ' <<p<<endl; fout<<a<<' ' <<b<<' ' <<p<<endl; } fout.close (); } void create_dataset () int n = random (2 , 400 ); int t = 1 ; while (t--) build (n); } bool work () create_dataset (); system ("stand.exe < input.txt" ); system ("my.exe < input.txt" ); return system ("fc stand.txt my.txt" ); } void dp (int tot) for (int i = 1 ; i <= tot; i ++ ) { cout << "正在运行第" << i << "个数据" << endl; if (work ()){ cout << "出错了\n" ; getchar (); } } } int main () srand (time (nullptr )); dp (512 ); cout << "Done" ; return 0 ; }
这道题算不上太难,但因为实现细节有很多,算上Floyd一共做了3次dp,补题的时候包括写对拍程序一共做了两个晚上,每次对拍都会出现不少没有考虑到的情况,第一次的时候没有考虑到存在中途回去睡觉可以是最优解的情况,之后的几次都是在代码的细节上出错,比如dp[i][course[j].p]写成dp[i][j]等,而且是在有clion的静态代码分析的情况下写了这么久,比赛时devc++没有分析和代码补全功能,所以在那种环境下更有可能没处理好拿好几次罚时。
G. Puzzle: Kusabi
Grammy是个拼图高手。今天,她正在玩“Kusabi”拼图的变体。在这个变体中,有一棵有根的树,上面有一些汉字。树的根是顶点1,没有标记。有标记的顶点可以有“长”、“短”或“同”的符号。其目标是将所有标记的顶点连接成对,以便:接下来的n-1行中的每一行都包含两个整数i,$p_i$和字符串$t_i(t_i\in \left \{ chang,duan,tong,- \right \} )$表示在$p_i$和i之间有一条边,以及顶点的类型I是$t_i$”_”表示未标记顶点i)。保证i是按递增顺序给出的。还保证至少有一个标记的顶点。oj 的评测
贪心题:d[u]数组:存储当前结点对应的深度ver[u]数组:存储当前结点对应的种类,0表示不是特殊点,1-3表示“Duan”“Chang”“Tong”,三种状态remain[u]数组:存储当前结点的儿子们有无剩余的未配对的结点,数值同ver数组num[u][i]数组:存储当前u结点下包括自身的所有状态为i的结点个数edge[N]数组:邻接表存图v[i]vector数组:存储当前子树所有没有配对的结点,并可由size()统计个数flag变量:表示当前是否有无解的状态
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 #include <bits/stdc++.h> using namespace std;const int N = 1000005 ;typedef pair<int , int > PII;int d[N], ver[N], remain[N], num[N][4 ], n;bool flag = true ;char s[10 ];vector<PII> ans; vector<int > edge[N]; void dfs (int u, int par) vector<int > v[4 ]; d[u] = d[par] + 1 ; ++num[u][ver[u]]; for (int i = 1 ; i <= 3 ; ++i) if (ver[u] == i)v[i].push_back (u); for (auto &ne: edge[u]) { if (ne == par) continue ; dfs (ne, u); for (int i = 1 ; i <= 3 ; ++i) if (ver[remain[ne]] == i) v[i].push_back (remain[ne]); for (int i = 1 ; i <= 3 ; ++i) num[u][i] += num[ne][i]; } if (!flag) return ; if (abs (num[u][1 ] - num[u][2 ]) >= 2 ) { flag = false ; return ; } if (num[u][1 ] != num[u][2 ] && (num[u][3 ] & 1 )) { flag = false ; return ; } for (int i = 1 ; i <= 3 ; ++i) sort (v[i].begin (), v[i].end (), [&](const int u, const int v) { return d[u] < d[v]; }); int v1 = (int ) v[1 ].size (), v2 = (int ) v[2 ].size (), v3 = (int ) v[3 ].size (); for (int i = 0 ; i < v3; i += 2 ) { if (i == v3 - 1 ) { remain[u] = v[3 ][i]; break ; } if (d[v[3 ][i]] != d[v[3 ][i + 1 ]]) remain[u] = v[3 ][i++]; ans.emplace_back (v[3 ][i], v[3 ][i + 1 ]); } if (num[u][1 ] > num[u][2 ]) { int l = v1 - 1 , r = v2 - 1 ; while (l >= 0 || r >= 0 ) { if (l >= 0 && r >= 0 && d[v[1 ][l]] < d[v[2 ][r]]) { ans.emplace_back (v[1 ][l--], v[2 ][r--]); } else if (!remain[u] && l >= 0 ) { remain[u] = v[1 ][l--]; } else { flag = false ; return ; } } } else { int l = 0 , r = 0 ; while (l < v1 || r < v2) { if (l < v1 && r < v2 && d[v[1 ][l]] < d[v[2 ][r]]) { ans.emplace_back (v[1 ][l++], v[2 ][r++]); } else if (!remain[u] && r < v2) { remain[u] = v[2 ][r++]; } else { flag = false ; return ; } } } } int main () cin.tie (nullptr ), cout.tie (nullptr ); ios::sync_with_stdio (false ); cin >> n; for (int i = 1 , u, v; i < n; ++i) { cin >> u >> v >> s; edge[u].push_back (v), edge[v].push_back (u); if (s[0 ] == 'D' )ver[u] = 1 ; if (s[0 ] == 'C' )ver[u] = 2 ; if (s[0 ] == 'T' )ver[u] = 3 ; } dfs (1 , 0 ); if (!flag || remain[1 ]) cout << "NO\n" ; else { cout << "YES\n" ; for (auto &it: ans) cout << it.first << ' ' << it.second << '\n' ; } return 0 ; }
树上贪心问题,这题的贪心策略并不算好想,也融合了树的遍历,树形dp的思想,由于树这种结构天然的适合dp和递归,所以题目就算没有要用树形dp去解也要考虑是否可以利用这个特殊的结构去实现算法,这道题的坑点也很多,像没看到每条边只能经过一次这个条件就会误以为是很简单的一道贪心题,最后关于“Tong”结点的处理也不好想到,很难在短时间内验证正确性
H. Puzzle: Tapa
翻译:oj 的评测
这题的通过率低到离谱,是除了只有一队通过的C题以外最低的一题,原因可能是题目只说了每个线索单元格表示其周围连续阴影单元格的数量,没有说明要涂色的点必须是联通的,像
1 2 3 4 5 6 7 8 3 3 3.2 .3 ..... 5.7 .5 ..... 3.5 .3 output: NO
如果理解为涂色点可以不联通只要最多的联通数量等于给的线索那么输出会是
1 2 3 4 5 6 7 YES 3 3 3 #2 #3 ##.## 5 #7 #5 ##### 3.5 .3
由于要求连续,所以有一个很重要的结论:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 #include <bits/stdc++.h> #define N 1505 using namespace std;typedef pair<int , int > PII;vector<int > edge[N]; int n, m, v[N];bool st[N];vector<PII> vl, vr; bool find (int x) st[x] = true ; for (auto y: edge[x]) { if (v[y] == -1 || (!st[v[y]] && find (v[y]))) { v[y] = x; return true ; } } return false ; } int match (int num) int ans = 0 ; memset (v, -1 , sizeof v); for (int i = 0 ; i < num; ++i) { memset (st, false , sizeof st); if (find (i)) ++ans; } return ans; } int main () cin.tie (nullptr ), cout.tie (nullptr ); ios::sync_with_stdio (false ); cin >> n >> m; vector<string> mat (2 * n - 1 ) ; for (auto &s: mat) { cin >> s; for (auto &c: s) if (c == '.' ) c = '#' ; } for (int i = 0 ; i < n; ++i) for (int j = 0 ; j < m; ++j) { char t = mat[2 * i][2 * j]; if (t == '3' || t == '5' || t == '8' )continue ; if ((i + j) % 2 == 0 )vl.emplace_back (i, j); else vr.emplace_back (i, j); } int v1 = (int ) vl.size (), v2 = (int ) vr.size (); if (v1 != v2) return cout << "NO\n" , 0 ; for (int i = 0 ; i < v1; ++i) { auto [x1, y1] = vl[i]; for (int j = 0 ; j < v2; ++j) { auto [x2, y2] = vr[j]; int dist = abs (x1 - x2) + abs (y1 - y2); bool isBoundary = (x1 == 0 && x2 == 0 ) || (x1 == n - 1 && x2 == n - 1 ) || (y1 == 0 && y2 == 0 ) || (y1 == m - 1 && y2 == m - 1 ); bool isIntern = mat[2 * x1][2 * y1] == '7' && mat[2 * x2][2 * y2] == '7' ; if (dist == 1 && (isBoundary || isIntern)) edge[i].push_back (j); } } if (match (v1) != v1) cout << "NO\n" ; else { cout << "YES\n" ; for (int i = 0 ; i < v2; ++i) { auto [x2, y2] = vr[i]; int j = v[i]; auto [x1, y1] = vl[j]; mat[x1 + x2][y1 + y2] = '.' ; } for (auto &s: mat) cout << s << '\n' ; } return 0 ; }
可以像注释里的代码一样定义一个结构体,将所有的初始化,数组长度在结构体初始化的时候申请对应的大小就可以保证空间也不会被浪费。
I. Equation Discovering
翻译:
Mika教授是一位计算机科学研究人员,他提出了以下问题:给定n对(x,y),其中1≤n≤20,我们如何找到适用于所有对的控制方程y=f(x)?换句话说,他试图确定一个方程,该方程涉及二元运算符(+,-,x,÷)、一元运算符(sin,cos)、符号x和适用于所有给定对的括号,例如y=xx÷sin(x)或y=x (x+x÷x)。
为了生成所有有效的方程,我们定义了一个上下文无关语法,如下所示:
1.起始符号为S。
2.S→S+S | S-S
3.S→SxS | S+S
4.S→sin(S) | cos(S)
5.S→(S) l x
然而,为了防止过拟合,我们将方程的复杂度限制为小于或等于9,其中复杂度定义为二元运算符(+,-,x,÷)数量的两倍加上方程中一元运算符(sin,cos)数量的一倍。例如,方程x+(x+xx)的复杂度为6,而x sin()的复杂程度为3。只有复杂度小于或等于9的方程才会被认为是正确的。
输入
第一行包含一个整数n(1≤n≤20),表示要拟合的(x,y)对的数量。以下n行,每行两个实数r,y(zl,<103),小数点后正好有六位数字,表示(x,y)对。
x的值保证是准确的,我们使用一些有效的方程来生成y的值,然后将其四舍五入到六位数。
输出
输出只有一行表达式f,由’+’、-’、*’(对于x)、/’(对于÷)、’sin’、’cos’、’x’、(’和)’组成。
如果您的答案满足以下条件,则视为正确:
1.表达式f是使用前面描述的上下文无关语法生成的,并且根据该语法是有效的。
2表达式f的复杂度不超过9,并且长度不超过1000个字符。
3.对于每个(z,y)对,f(z)和g之间的绝对或相对误差不大于10
3。即≤10-3
4.在计算除法运算时,被除数的绝对值必须不小于0.01。
留坑待填
赛后总结 …没去颁奖现场也没找到获奖率的通知,文件里面只写了这些:
比赛时做了AEFM四道题,按照这个规则来看,如果要拿铜必须要做得快,银牌需要做出K题,做出G题稳银,再做出H题稳金。
比赛的排名规则 首先按解题数量排序,每道题权值一样,解题数量越多的排在前面,题数一样多的队伍按时间排(表中的score),时间的具体计算是:每道题第一次ac的时间(单位为分钟)的总和加上已ac的题目中先前提交wa的次数20。像我们队解出AEMF的时间分别是比赛开始后的10,49,95,210,其中F题罚时一次,那么总时间就是10+49+95+210+20 1 = 384,所以四题里用时比我们长的都排在后面








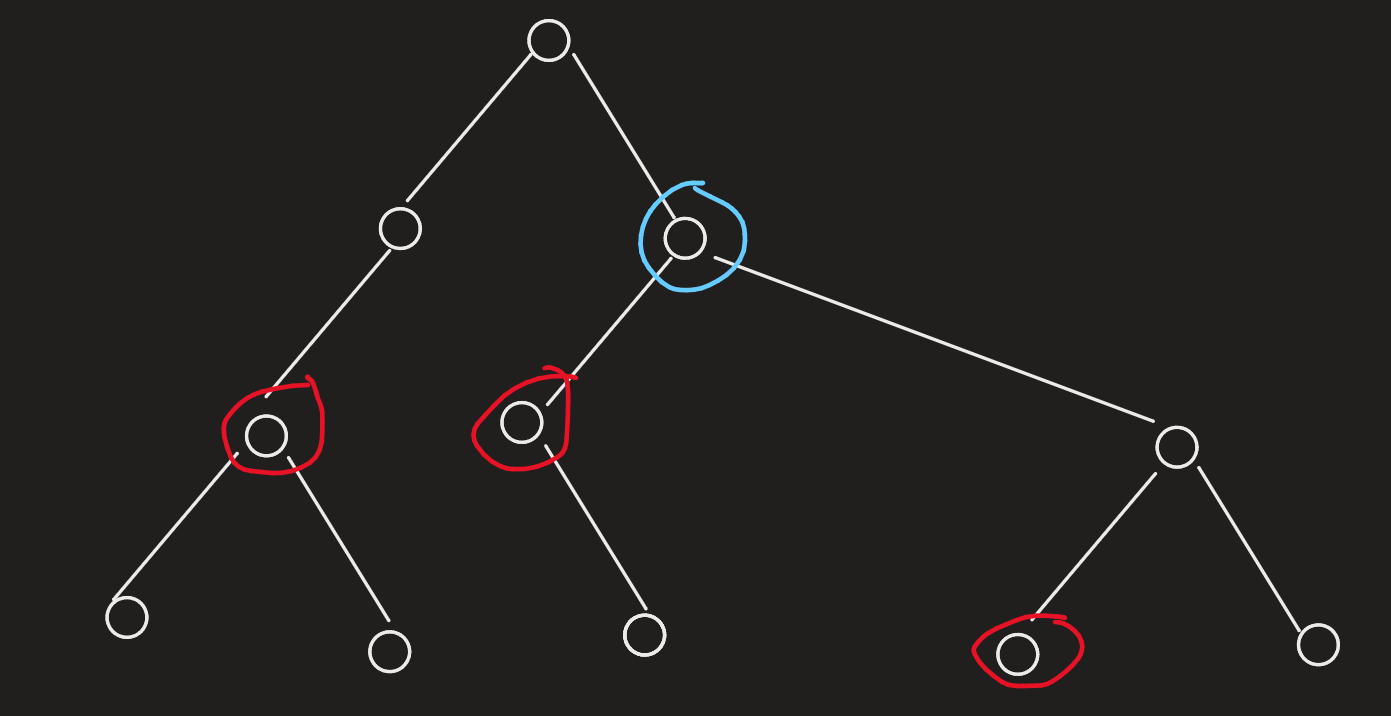
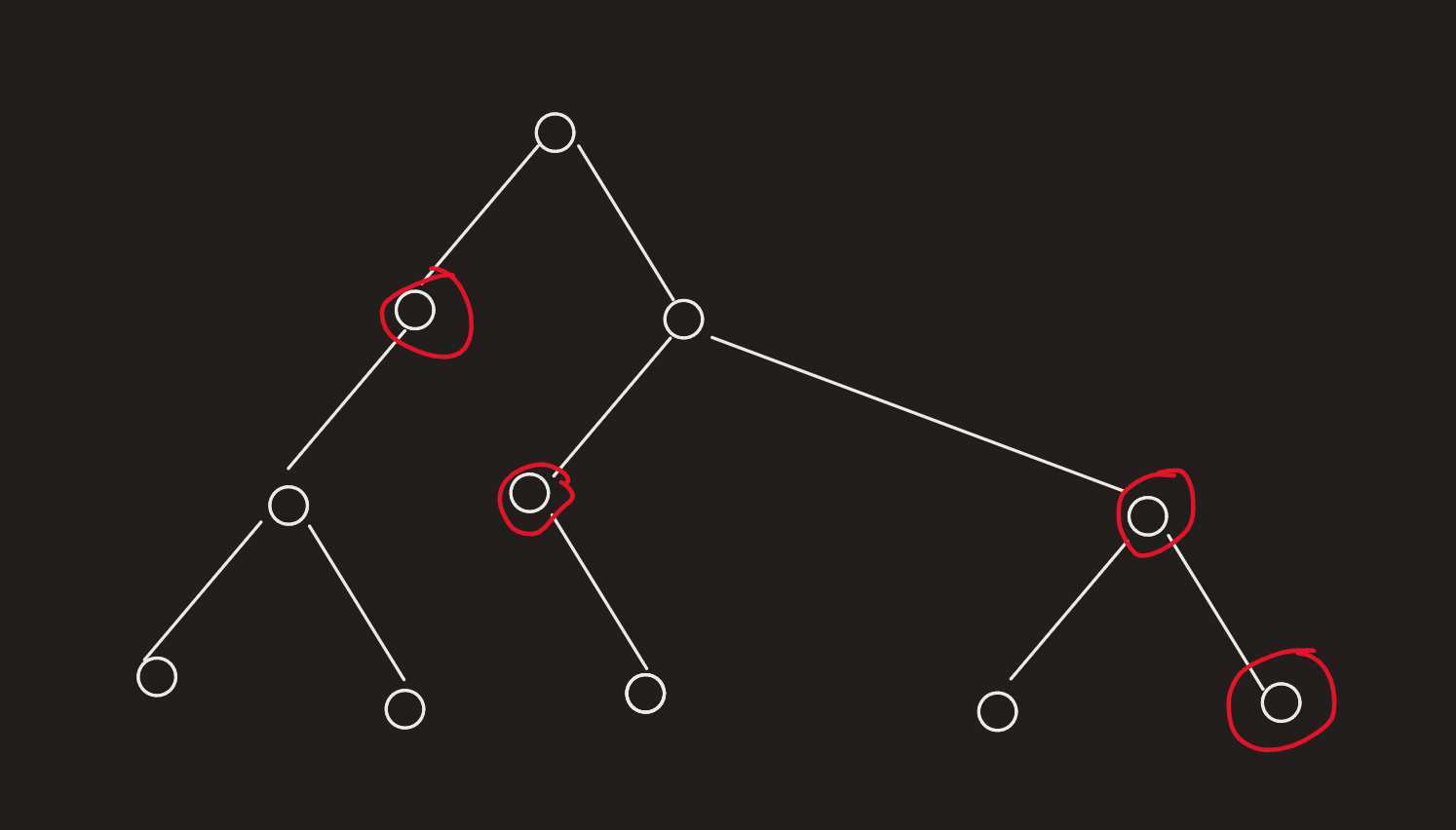 红点表示“Tong”蓝点表示不是“Tong”的标记点,第一张图表明第一种无解情况,第二张表明第二种无解情况,注意并不需要特地判断当前子树是不是存在两个及以上的无法配对的情况,证明需要根据奇偶性分四类讨论:
红点表示“Tong”蓝点表示不是“Tong”的标记点,第一张图表明第一种无解情况,第二张表明第二种无解情况,注意并不需要特地判断当前子树是不是存在两个及以上的无法配对的情况,证明需要根据奇偶性分四类讨论: