题面：

C - easy math

给出一个长度为n整数数组a。数组a中的每一个整数$ a_i $都是2的幂。求满足$ \prod_{i=1}^{n} a_i \leq 2024^b $的最小整数b。

注意到每个数都是2的幂所以可以直接对每个元素取对数让乘法变加法，最后直接用换底公式搞一下2024的b次方把b提出来就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void solve(){
    int n;
    cin>>n;
    vector<int> a(n);
    int sum = 0;
    for(int i = 0;i<n;++i){
        cin>>a[i];
        a[i] = (int)log2(a[i]);
        sum += a[i];
    }
    long double base = log(2024),p = log(2);
    long double logg = p/base;
    int ans = (ceil)(sum * logg);
    cout<<ans<<endl;
}

C要处理高精度所以要想想对数，贴个python，可以直接用python写这样就不用动脑子了

1
2
3
4
5
6
7
8
9
10
11
import math

n = int(input())
str = input()
a = str.split()
t = 1

for i in a:
    t *= int(i)

print(math.ceil(math.log(t,2024)))

xcpc要是真敢出高精度估计选手能让出题人飞起来

I - 数据检索系统

按题意模拟即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
bitset<N> st;

void solve(){
    int n,k,m,q;
    cin>>n>>k>>m>>q;
    for(int i = 0;i<m;++i){
        int t;
        cin>>t;
        int temp = t % n;
        for(int j = 1;j<=k;++j){
            st[temp] = 1;
            temp *= t;
            temp %= n;
        }
    }

    //	for(int i = 0;i<n;++i) cerr<<st[i]<<" \n"[i == n-1];

    for(int i = 0;i<q;++i){
        int t;
        cin>>t;
        int temp = t % n;
        bool ok = true;
        for(int j = 1;j<=k;++j){
            //			st[temp] = 1;
            ok &= st[temp];
            temp *= t;
            temp %= n;
        }
        cout<<ok<<' ';
    }
    cout<<endl;
}

E - 拼接串

注意到每个数都只能出现一次，这就容易想到每种状态都是独立的互不干扰的且$ a_i $很小只有18种，每种状态对应的都是选与不选，就可以往状态压缩方向去想了。

那么首先就是怎么不重不漏的找出状态。先定义dp[s]表示有没有区间是s这个状态的并记录下集合s中的数字个数，因为18种，n范围由是1e6，18*1e6又是符合时限的，考虑在枚举的过程中每个位置操作大约20次的实现，因为要求是不能重复的所以可以想到直接每个位置往后枚举一遍，每次在枚举的时候更新状态。

比如样例一，第一个位置，2，然后继续往后遍历到出现重复数字为止也就是第三位为止出现了两个1，那么更新$ dp[(0…11)_2]=max(1,dp[(0…11)_2],2) $表示s = 000…11（即包含1和2的这个集合）被更新一次。

通过这样的遍历就能尽可能的得到每个子区间的最大集合。

题目要求是两个区间相加，那么可以将问题转化为枚举一个集合，找它的补集以及补集的子集中最多的那个，那么问题就转化为了如何找补集以及补集的子集中最多的那个。

可以考虑区间从小到大合并，比如只有一个数字的集合肯定是这个集合和只有0个数字的集合取max，有两个数字的集合一定是自己本身和只有1个数字集合取max，这样就大概能在$ O(18*2^{18}) $的复杂度预处理出每一个集合以及它的子集中最多的那个。

然后就是枚举每一个集合和它的补集以及补集的子集中最多的那个相加取最大就是答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
const int M = (1ll<<18);
 
void solve() {
	int n;
	cin >> n;
	vector<int> a(n);
	for (int i = 0; i < n; ++i) cin >> a[i];
	vector<int> dp(M);
	for(int i = 0;i<n;++i){
		int j = i;
		set<int> st;
		int bit = 0;
		while(j < n && !st.count(a[j])){
			st.insert(a[j]);
			bit += (1ll<<(a[j]-1));
			j++;
			dp[bit] = max(dp[bit],si(st));
		}
	}
//	for(int i = 0;i<16;++i) cerr<<dp[i]<<' ';
//	cerr<<endl;
	for(int i = 1;i<M;++i){
		int tot = i;
		for(int j = 0;j<=18;++j){
			if(tot & (1ll<<j)){
				int k = tot - (1ll<<j);
				dp[i] = max(dp[k],dp[i]);
			}
		}
	}
//	for(int i = 0;i<16;++i) cerr<<dp[i]<<' ';
//	cerr<<endl;
	int ans = 0;
	for(int i = 1;i<M;++i){
		int s = i;
		int antis = ((1ll<<18) - 1)^s;
		ans = max(dp[s] + dp[antis],ans);
//		cerr<<ans<<' '<<s<<':'<<' '<<dp[s]<<' '<<antis<<':'<<' '<<dp[antis]<<endl;
	}
	cout<<ans<<endl;
}

K - 渡劫

vp的时候没想到分层图当时只是随口提了一句：我觉得好像可以每条边额外加一条为0的边但是不知道怎么处理。然后就直接牢了。知道这东西还是很简单的。

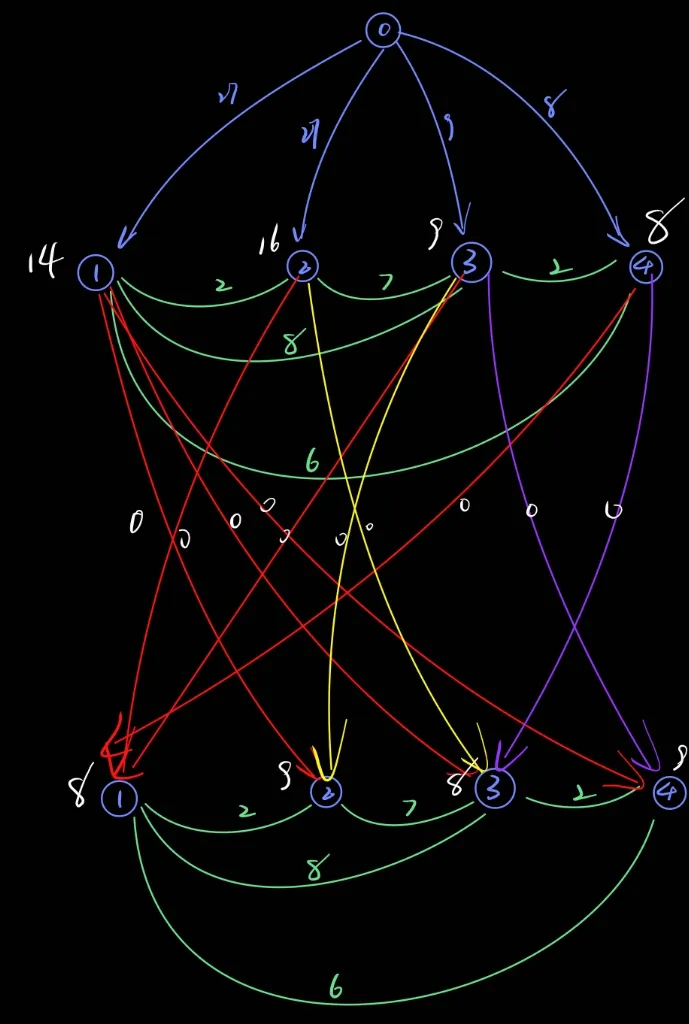
先简化条件，不考虑法宝，假设初始传送在i号岛屿，最终在j号岛屿上，那么所需要的能量是dist[i->j] + a[j]，考虑建一个超级源点从源点反向跑每一个点，这样就能转化为单源最短路问题，一遍dij之后再对所有的dist取一个max就能得到至少要的能量。

然后有一次免费的机会，这种带条件的最短路就应该往分层图上去想，比如这道板题：P4568[JLOI2011] 飞行路线。

建图的时候，把第二层表示为用掉一次免费的机会，比如在从u走到v的时候用掉了法宝，就可以表示为从第一层的u连向第二层的v，边权为0。

1
2
3
4
5
6
7
4 5
3 2 7
4 1 6
3 4 2
2 1 2
3 1 8
27 27 9 8

跑一遍dij就没了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
struct SP {
	struct Edge {
		int to{};
		int w{};

		Edge(int a, int b) {
			to = a;
			w = b;
		}
	};

	typedef pair<int, int> PII;
	int n{}, s{};
	vector<vector<Edge>> edge;
	vector<int> dist;
	vector<bool> st;

	SP(int _n, int _s): n(_n), s(_s), edge(_n + 1), dist(_n + 1), st(_n + 1) {};

	void dijkstra() {
		fill(all(dist), 4e18);
		dist[s] = 0;
		priority_queue<PII, vector<PII>, greater<>> heap;
		heap.emplace(0, s);
		while (!heap.empty()) {
			auto ver = heap.top().second;
			heap.pop();
			if (st[ver]) continue;
			st[ver] = true;
			for (auto &i : edge[ver]) {
				int j = i.to;
				if (dist[j] > dist[ver] + i.w) {
					dist[j] = dist[ver] + i.w;
					heap.emplace(dist[j], j);
				}
			}
		}
	}
};

void solve() {
	int n, m;
	cin >> n >> m;
	SP dij(n * 2, 0);
	for (int i = 0, u, v, w; i < m; ++i) {
		cin >> u >> v >> w;
		for (int j = 0; j <= 1; ++j) {
			if (j) dij.edge[u + (j - 1) * n].emplace_back(v + j * n, 0);
			if (j) dij.edge[v + (j - 1) * n].emplace_back(u + j * n, 0);
			dij.edge[u + j * n].emplace_back(v + j * n, w);
			dij.edge[v + j * n].emplace_back(u + j * n, w);
		}
	}
	for (int i = 1, w; i <= n; ++i) {
		cin >> w;
		dij.edge[0].emplace_back(i, w);
	}
//	自己在自己这个岛上渡劫，不连接的话那么对于ans的求法会出问题，
//	因为下面这个ans的写法强制要求一定要用掉一次法宝，即不能在自己这个岛上渡劫
	for (int i = 1; i <= n; ++i) dij.edge[i].emplace_back(i + n, 0);
	dij.dijkstra();
	int ans = 0;
	for (int i = 1; i <= n; ++i) ans = max(dij.dist[i + n], ans);
//	for (int i = 1; i <= n; ++i) cerr << dij.dist[i + n] << " \n"[i == n];
//	for (int i = 1; i <= n; ++i) cerr << dij.dist[i] << " \n"[i == n];
	cout << ans << endl;
}

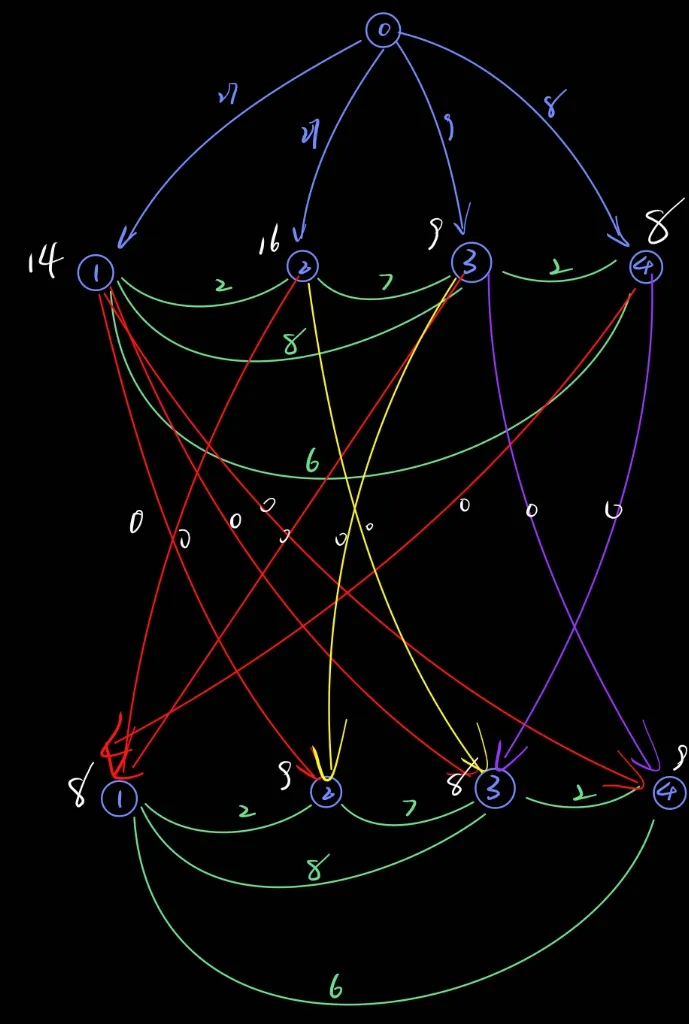
需要注意的是这个像下面这样的实现需要考虑在自己这个岛上渡劫的情况，比如

1
2
3
4
5
6
7
8
5 6
1 2 3
1 3 1
2 4 2
2 5 4
3 4 1
4 5 3
10 5 2 7 12

那么dist的情况：

1
2
第一层dist[1-5]:3 5 2 3 6
第二层dist[1-5]:2 3 3 2 3

发现dist[3]在用了法宝花费还变多了，原因在于我在统计答案的时候必须要用一次移动而没有考虑在自己岛上直接渡劫的情况。所以对于样例一的图应该还要再加上连向自己的边。

当然直接把ans改为ans = max(min(dij.dist[i + n],dij.dist[i]), ans);也可以。

复杂度大概是$ O(2nlog2m) $。不知道这开个2.5s的时限是在暗示什么……分层图不熟还往双log的算法方向想了半天。

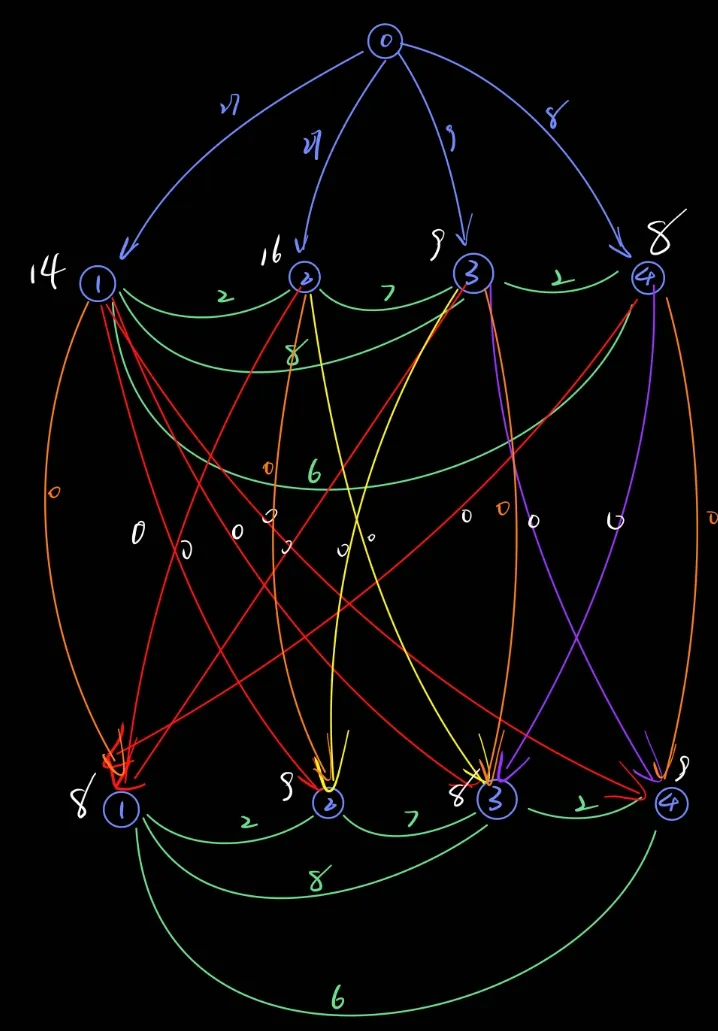
可以把分层图的操作用数组存下来用一种类似于dp的记忆化存储状态。

注意到这张图在连向第二层的时候是有向边，也就是说在这一步转移的时候是有顺序的，符合dp的原则，可以考虑把这一步用dp的思想来转移。

定义dist[i][j]表示是第i个点，j == 0的时候是没用过，j == 1的时候是用过法宝了

从i号点走到j号点，对于这一张图有三种情况：
1.没用过走到没用过的点->dist[j][0] = dist[i][0] + w

2.没用过走到用过的点,即这次用了法宝->dist[j][1] = dist[i][0] + 0

3.用过走到用过的点 -> dist[j][1] = dist[i][1] + w

注意第二种情况只有不是0号源点的时候是存在的对应到图上就是因为0号点没有连向第二层图的边。

其他就是正常的dij贪心。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
struct SP {
	struct Edge {
		int to{};
		int w{};

		Edge(int a, int b) {
			to = a;
			w = b;
		}
	};
	typedef tuple<int, int, int> PIII;
	int n{}, s{};
	vector<vector<Edge>> edge;
	vector<array<int, 2>> dist;
	vector<array<bool, 2>> st;
	SP(int _n, int _s): n(_n), s(_s), edge(_n + 1), dist(_n + 1, array<int, 2> {0, 0}), st(_n + 1,array<bool, 2> {false,false}) {};

	void dijkstra() {
		const int temp = 4e18;
		fill(all(dist), array<int, 2> {temp, temp});
		dist[s][0] = 0;
		priority_queue<PIII, vector<PIII>, greater<>> heap;
		heap.emplace(0, s, 0);
		while (!heap.empty()) {
			auto [fi, ver, kind] = heap.top();
			heap.pop();
			if (st[ver][kind]) continue;
			st[ver][kind] = true;
			for (auto &i : edge[ver]) {
				int j = i.to;
				if (kind == 0) {
					if (dist[j][0] > dist[ver][0] + i.w) {
						dist[j][0] = dist[ver][0] + i.w;
						heap.emplace(dist[j][0], j, 0);
					}
					if (ver != 0 && dist[j][1] > dist[ver][0]) {
						dist[j][1] = dist[ver][0];
						heap.emplace(dist[j][1], j, 1);
					}
				} else {
					if (dist[j][1] > dist[ver][1] + i.w) {
						dist[j][1] = dist[ver][1] + i.w;
						heap.emplace(dist[j][1], j, 1);
					}
				}
			}
		}
	}
};

void solve() {
	int n, m;
	cin >> n >> m;
	SP dij(n, 0);
	for (int i = 0, u, v, w; i < m; ++i) {
		cin >> u >> v >> w;
		dij.edge[u].emplace_back(v, w);
		dij.edge[v].emplace_back(u, w);
	}
	for (int i = 1, w; i <= n; ++i) {
		cin >> w;
		dij.edge[0].emplace_back(i, w);
	}

	dij.dijkstra();
	int ans = 0;
	for (int i = 1; i <= n; ++i) ans = max(min(dij.dist[i][0], dij.dist[i][1]), ans);
	cout << ans << endl;
}

A - 贪吃蛇

感觉A题还比其他后面的题要简单些不知道为什么过的人这么少

首先注意到这个n是很小的，允许做一些像是枚举线段这样很暴力的处理。

因为可以旋转坐标系，那么贪心的想，以零点到任意一个点作为x轴方向就能尽可能多的吃到金币。

这两点就允许了做一个$ O(n^2) $的枚举方向线段。

通过枚举就得到了一个方向线段，注意到和一般的不一样的是这个蛇可以在两个分量上移动任意的距离，这说明分成两种情况，一种是和这个线段夹角成[0°,90°]以内的，另一种是和这个线段夹角成[-90°，0°]以内的，这两种分开讨论只要满足以这条线段为初始的方向在[0°,90°]（或[-90°，0°]）的点，他们构成的线段都有机会是蛇的移动路线，吃的多那就是贪吃蛇的移动路径最长。

所以就可以想到建图，用方向来连边，如果两个点都在[0°,90°]（或[-90°，0°]）的范围内并且构成的有向线段的方向是和初始线段的方向夹角小于[0°,90°]（或[-90°，0°]）那么就是允许这个点连向另一个点，这样就就能不重不漏的枚举每一种情况。

判断方向可以用向量的点乘和叉乘，如果向量a和b点乘和叉乘都是大于0的那么说明a和b的夹角小于90°并且b位于a的逆时针方向，如果点乘大于0叉乘小于0说明b位于a的顺时针方向。

样例给的还有点良心注意如果如果金币在原点就有的话（样例一）还要对这个特殊点进行处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
void solve() {
	int n;
	cin>>n;
	vector<PII> p;
	p.push_back({0,0});
//	for(int i = 1;i<=n;++i) cin>>p[i].fi>>p[i].se;
	bool f = false;
	for(int i = 1,x,y;i<=n;++i){
		cin>>x>>y;
		if(x == 0 && y == 0){
			n--;
			i--;
			f = true;
		}else{
			p.push_back({x,y});
		}
	}
	
	int ans = 0;
	
	auto dot = [&](const PII &a, const PII &b) {
		return a.fi * b.fi + a.se * b.se;
	};
	
	auto cross = [&](const PII &a, const PII &b) {
		return a.fi * b.se - a.se * b.fi;
	};
	
	auto ve = [&](PII a,PII b){
		return PII{a.fi - b.fi,a.se - b.se};
	};
	
	auto isok = [&](PII st,PII a,PII b,int clockwise){
		bool ok = true;
		ok &= (dot(st,a) >= 0) && (cross(st,a) * clockwise >= 0);
		ok &= (dot(st,b) >= 0) && (cross(st,b) * clockwise >= 0);
		ok &= (dot(st,ve(a,b)) >= 0) && (cross(st,ve(a,b)) * clockwise >= 0);
		return ok;
	};
	
	auto bfs = [&](PII ve,int clockwise){
		vector<int> dis(n+1,0ll),deg(n+1,0ll);
		vector<vector<int>> edge(n+1);
//		都在同一侧，那么就可以连一条边
		for(int i = 0;i<=n;++i)
			for(int j = 0;j<=n;++j){
				if(i == j) continue;
				if(isok(ve,p[i],p[j],clockwise)) edge[j].push_back(i),deg[i]++;
			}
//		for(int u = 0;u<=n;++u){
//			cerr<<u<<":\n";
//			for(int v : edge[u]) cerr<<v<<" \n"[v == edge[u].back()];
//		}
//		
//		for(int i = 0;i<=n;++i) cerr<<deg[i]<<" \n"[i == n];	
//		拓扑跑最长路
		queue<int> q;
		q.push(0);
		while(!q.empty()) {
			auto u = q.front();
			q.pop();
			for (auto v : edge[u]) {
				dis[v] = max(dis[v],dis[u] + 1);
//				deg[v]--;
				if(--deg[v] == 00) q.push(v);
//				if(deg[v] == 0) q.push(v);
			}
		}
		for(auto i : dis) ans = max(ans,i);
	};
	for(int i = 0;i<=n;++i)
		for(int j = 0;j<=n;++j){
//			枚举线段
			if(j == i) continue;
			PII t = ve(p[i],p[j]);
//			debug
//			cerr<<t.fi<<' '<<t.se<<endl;
//			分两个方向建图，负方向对应关于t的翻转
			bfs(t,1);
//			cerr<<ans + f<<endl;
//			debug
			bfs(t,-1);
//			cerr<<ans + f<<endl;
//			debug
		}	
//	for(int i = 0;i<n;++i) cerr<<dis[i]<<" \n"[i == n - 1];
	cout<<ans + f<<endl;
}